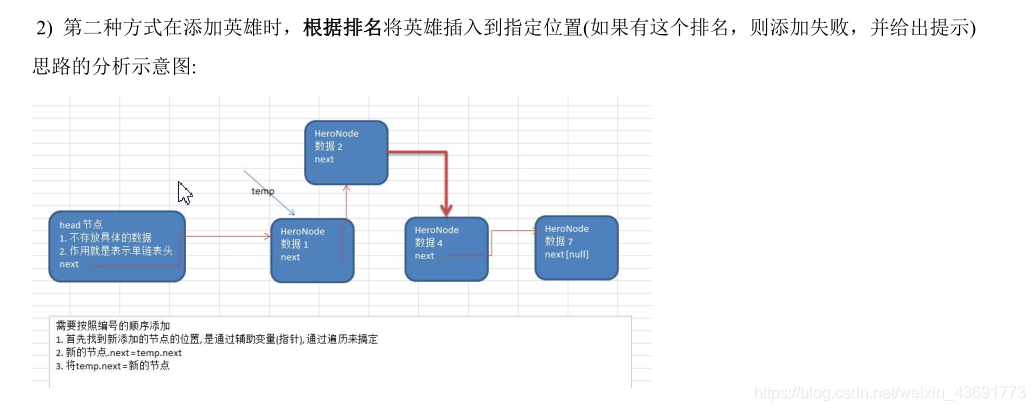
链表

LinkedList是双链表

  1. 链表是以节点的方式来存储, 是链式存储
  2. 每个节点包含 data 域， next 域：指向下一个节点.
  3. 如图：发现 链表的各个节点不一定是连续存储.
  4. 链表分 带头节点的链表和 没有头节点的链表，根据实际的需求来确定

单链表

就是单向的，有next–指向下一个节点

在这里插入图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
package 数据结构;


/*链表的生成
        ps:对于单链表，需要使用头插法和尾插法建立链表
        判断链表是否为空----node.next!=null
        链表的清空----node.next = null
        结点的插入
        结点的删除
        返回第 i 个结点
        返回链表的结点个数----遍历然后不断自增
        根据给定值，返回该值在链表出现的第一个位置---通过遍历自增 当找到时就返回下标
        */

public class SingleLinkedList {
    public static void main(String[] args) {

        Node Node1 = new Node(1);
        Node Node2 = new Node(2);
        LinkedList linkedList = new LinkedList();
        linkedList.addFirstNode(Node1);
        linkedList.add(Node2);
        System.out.println(linkedList.getValue(2).toString());
    }

    static class LinkedList {
        private Node head = new Node(0,null);

        // 尾插法
        // 1. 找到当前链表的最后节点
        // 2. 将最后的这个节点的next 指向 新节点
        public void add(Node Node){
            // 因为 head节点不能动 我们需要一个辅助节点 temp
            Node temp = head;
            // 遍历链表找到最后
            while (temp.next!=null){
                temp = temp.next;
            }
            // 当退出white循环时, temp 就指向了链表的最后
            temp.next = Node;
        }


          //头插法添加节点
        public void addFirstNode(Node Node) {
            Node node = head;
            node.next = Node;
        }

        //删除节点
        //1、可以让要删的前面的节点指向后一个节点就可以了，不过要遍历找到前面的那个节点
        //2、这里采用的是把要删除的下一个节点赋值给要删除的节点然后让该节点直接指向要删除的下下个节点
        // 这样是实现了对该节点数据的删除--只不过是通过对数据的迁移删除实现的--根据力扣题上的链表删除节点
        public void delNode(Node node){
            node = node.next;
            node.next = node.next.next;
        }

        //返回第 i 个结点
        public Integer getValue(int index){
            Node node = head;
            int i =0;
            while (node.next!=null){
                i++;
                if(i==index){
                    return node.no;
                }
                node = node.next;
            }
            return null;
        }
    }
    
    // 定义一个Node , 每个Node对象就是一个节点
    static class Node {
        public int no;
        public Node next; // 指向下一个节点

        // 构造器
        public Node(int No){
            this.no = No;
        }

        public Node(int No,Node next){
            this.no = No;
            this.next = next;
        }
    }
}

力扣反转链表

赋值符号是右边赋值给左边，超时的可能原因还有：方法体内需要的参数在体外赋值可能会超时

image-20220403121036296

这题注意参数的调用和读写，每个参数都有独特的意义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
//新链表
     ListNode newHead = null;
     while (head != null) {
         //先保存访问的节点的下一个节点，保存起来
         //留着下一步访问的
         ListNode temp = head.next;
         //每次访问的原链表节点都会成为新链表的头结点，
         //其实就是把新链表挂到访问的原链表节点的
        //后面就行了
       //下面两步不能调换，因为一开始新链表是尾部指向null的 然后才有头节点的更新
        head.next = newHead;
        //更新新链表
        newHead = head;
        //重新赋值，继续访问  不能是head.next因为前面已被赋值了 而每一次temp都被赋值成新的下一节点
        head = temp;
    }
    //返回新链表
        return newhead;
    }
}

顺序表和链表的优缺点

一、顺序表

  1. 顺序表的内存空间连续。
  2. 尾插、尾删效率较高，时间复杂度是O(1)。
  3. 支持随机访问，可以高效的按下标进行操作，时间复杂度是O(1)。

缺点：

  1. 在顺序表中间插入或删除元素时都涉及到元素的移动，效率较低，时间复杂度为O(N)。
  2. 顺序表长度固定，有时需要扩容。

二、链表：

优点

  1. 链表的内存空间不连续。
  2. 如果知道要处理节点的前一个位置，则进行插入和删除的复杂度为O(1);
  3. 如果不知道要处理节点的前一个位置，则进行插入和删除的复杂度为O(N)。
  4. 头插、头删的效率高，时间复杂度是O(1)。
  5. 没有空间限制，不会溢出，可以存储很多元素。

缺点：

链表不支持随机访问，查找元素效率低，需要遍历节点，时间复杂度是O(1)。

三、总结

  • 当线性表的长度变化不大、易于确定其大小时，采用顺序表作为存储结构。
  • 若线性表主要操作是查找。很少进行插入或删除操作时，采用顺序表作为存储结构。
  • 对于频繁进行插入和删除的线性表，则应该使用链表作为存储结构。

队列（queue）

队列：有序列表，可以用数组或链表实现，先入先出

以下为循环队列：

image-20220403190521859

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
package queue;

import java.util.Arrays;

public class MyQueue {
    private Integer[] queue;
    private int size = 0;//队列现存的数据个数
    private int front = 0;//队前索引
    private int rear = 0;//队尾索引

 
    /**
     * 构造方法
     *
     * @param length 队列大小
     */
    public MyQueue(int length) {
        //要预留一个位置给rear+1 供空间调配
        queue = new Integer[length + 1];
    }

    /**
     * 入队
     *
     * @param value 值
     */
    public void enQueue(int value) {
        if (isFull()) {
            throw new RuntimeException("Queue is full.");
        }
        queue[rear] = value;
        rear = (rear + 1) % queue.length;//rear要指向最后元素的下一个空闲位置
        size++;
    }

    /**
     * 出队
     *
     * @return 值
     */
    public Integer outQueue() {
        Integer res = queue[front];
        front = (front + 1) % queue.length;
        size--;
        return res;
    }


    /**
     * 获取队列头元素
     */
     public int Front() {
        if(isEmpty()){
            return -1;
        }else{
            return queue[front];
        }
    }
    
    /**
     * 获取队列尾部元素---重要
     */
    public int Rear() {
        if(isEmpty()){
            return -1;
        }else{
            return queue[(rear - 1 + queue.length) % queue.length];//队列长度
        }
    }
    

    /**
     * 清空队列
     */
    public void clear() {
        size = 0;
        front = 0;
        rear = 0;
        Arrays.fill(queue, null);
    }

    /**
     * 检查队列是否为空
     *
     * @return 是否为空
     */
    public boolean isNull() {
        return front == rear;
    }

       /**
     * 检查队列是否已满  rear右移发现与head重合了，则没有地方放入新的元素了，此时为满
     *
     * @return 是否已满
     */
    public boolean isFull() {
        return (rear + 1) % queue.length == front;
    }
    
    @Override
    public String toString() {
        if (isNull()) {
            return "null";
        }
        int i = front;
        String str = "";
        while (i != rear) {
            str += queue[i] + ",";
            i = (i + 1) % queue.length;
        }
        str = str.substring(0, str.length() - 1);
        return "MyQueueSequence{" + str + "}";
    }
}


//java内置有Queue的类 可以不用造轮子
// 1. Initialize a queue.
        Queue<Integer> q = new LinkedList();
        // 2. Get the first element - return null if queue is empty.
        System.out.println("The first element is: " + q.peek());
        // 3. Push new element. 入队
        q.offer(5);
        q.offer(13);
        q.offer(8);
        q.offer(6);
        // 4. Pop an element. 出队
        q.poll();
        // 5. Get the first element.
        System.out.println("The first element is: " + q.peek());
        // 7. Get the size of the queue.
        System.out.println("The size is: " + q.size());

image-20220403191825973

队列的真性和假性溢出

真溢出：Q.rear==Q.front

假溢出:当队列中的存储空间没满时，但是由于来的元素堵在队尾，此时如果还有元素要入队的话，就会报错，发生溢出

为了解决这个问题，有如下方法：

  1. 修改出队操作算法，使每次出队后都把队列中剩余的操作元素向队头移动一个位置；
  2. 修改入队算法,增加判断条件，当发生“假性溢出”时，把数据元素向队头移动；
  3. 采用循环队列；

栈（stack）

定义：先进后出，后进先出，限定仅在表尾进行插入和删除操作的线性表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
package it01;


public class stack {
    public static void main(String[] args) {
        ArrayStack stack =new ArrayStack(4);
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.push(4);
        stack.list();
    }

}

// 定义一个 ArrayStack 表示栈
class ArrayStack {
    private int maxSize; // 栈的大小
    private int[] stack; // 数组, 数组模拟栈 将栈的数据放入数组
    private int top = -1; //表示栈顶 初始化为-1

    // 构造器
    public ArrayStack (int maxSize) {
        this.maxSize = maxSize;
        stack = new int[this.maxSize];
    }

    // 栈满判断
    public boolean isFull() {
        return top == (maxSize-1);
    }

    // 栈空
    public boolean isEmpty() {
        return top == -1;
    }

    // 入栈的操作
    public void push (int value) {
        // 判断是否满
        if (isFull()){
            System.out.println("栈已经满了,无法入栈");
            return;
        }
        top++;
        stack[top] = value;
    }

    // 出栈 将栈顶的数据返回
    public int pop () {
        // 先判断栈是否空
        if (isEmpty()){
            throw new RuntimeException("栈空,没有数据");
        }
        return  stack[top--];
    }

    // 显示栈信息(遍历栈) 遍历时 需要从栈顶开始显示
    public void list() {
        if (isEmpty()) {
            System.out.println("栈空,没有数据");
            return;
        }
        int i = top;
        while (i >= 0){
            System.out.println(stack[i--]);
        }
    }

栈溢出

栈溢出的几种情况：

  1. 局部数组过大。当函数内部的数组过大时，有可能导致堆栈溢出。
  2. 递归调用层次太多。递归函数在运行时会执行压栈操作，当压栈次数太多时，也会导致堆栈溢出。
  3. 指针或数组越界。这种情况最常见，例如进行字符串拷贝，或处理用户输入等等。

栈的上溢与下溢

由于栈区域是在堆栈定义时就确定了的，因而栈工作过程中有可能产生溢出。栈溢出有两种情况可能发生：如栈已满，但还想再存入信息，这种情况称为栈上溢；另一种情况是，如栈已空，但还想再取出信息，这种情况称为栈下溢。

不论上溢或下溢，都是不允许的。因此在编制程序时，如果可能发生堆栈溢出，则应在程序中采取保护措施。这可以通过给SP规定上、下限，在进栈或出栈操作前先做SP和边界值的比较，如溢出则作溢出处理，以避免破坏其他存储区或使程序出错的情况发生。